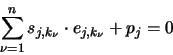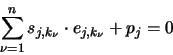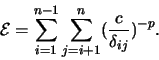Nächste Seite: Diskrepanzen auf der Kugel
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Symmetrische Lagerungen, Konstruktionen
Inhalt
Versucht man zu einer beliebigen Zahl n die optimale
Lagerung zu bestimmen, so entdeckt man bald, daß die bisher
aufgezeigten Methoden nicht ausreichen.
Liegt ein irreduzibler Graphen vor, so bedeutet das keineswegs, daß man
bereits die optimale Lagerung gefunden hat. Wie schwierig sich die Suche
nach dem optimalen Graphen für 9 Punkte gestaltet, kann man [76] entnehmen.
Daher sucht man generelle Verfahren, die feststellen, ob ein
vorliegender irreduzibler Graph optimal sein könnte.
Üblicherweise nimmt man dafür Anleihen aus der Physik.
Ein solches - allerdings umständliches - Verfahren fanden Danzer [24], sowie
Tarnai und Gáspár [88], [89].
Wichtig ist in diesem Verfahren der physikalischen Begriff
der ''Starrheit'' einer Lagerung, deren Graphen man sich als ein
festes ''"Stabwerk'' vorstellt. Dabei sind die Kanten des Graphen
als Stäbe und die Ecken des Graphen als verbindende Gelenke,
die keinerlei Reibung besitzen, aufzufassen. [Die exakten
Definitionen entnehme man der Literatur].
Es bezeiche 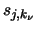 eine Kraft, die auf den Stab wirkt, der
zwischen den Punkten
eine Kraft, die auf den Stab wirkt, der
zwischen den Punkten 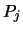 und
und 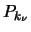 liegt. Ist s > 0, so ist der
Stab zug-, ansonsten ist er druckbeansprucht. Es sei
liegt. Ist s > 0, so ist der
Stab zug-, ansonsten ist er druckbeansprucht. Es sei 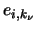 Einheitsvektor des Stabes, der
Einheitsvektor des Stabes, der 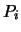 mit
mit 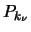 verbindet, und
verbindet, und 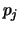 sei
eine im Knotenpunkt j angreifende Kraft [81], [88].
sei
eine im Knotenpunkt j angreifende Kraft [81], [88].
Das System befindet sich im Gleichgewicht [81,88], wenn gilt:
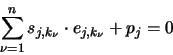 |
(1.22) |
Wenn wir die Gleichgewichtsmatrix G einführen und die
auftretenden Kräfte als Vektoren anschreiben, so ist dies gleich:
 |
(1.23) |
Die Gleichgewichtsmatrix G besteht aus k Spalten und 2n-3
Zeilen. [Im Graphen wäre k die Anzahl der Kanten [=Stäbe] und n
die Anzahl der Punkte.] Sie läßt sich in einfacher Weise aus
den Knotenkoordinaten berechen:
Sind die Punkte 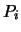 und
und 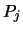 miteinander verbunden, so schreiben
wir an der Stelle (i,j) eine 1, ansonsten eine 0. In einer
Spalte können daher nur zwei Einsen stehen.
miteinander verbunden, so schreiben
wir an der Stelle (i,j) eine 1, ansonsten eine 0. In einer
Spalte können daher nur zwei Einsen stehen.
Jede (auch nur unendlich kleine) Veränderung des Stabwerkes
läßt sich ebenfalls mit einer Matrixgleichung anschreiben.
Genaueres findet sich im Buch von Szabó [81].
Tarnai und Gáspár [88, 89, 93] erhalten aus Falluntersuchungen
über den Rang der Matrix G, daß eine Lagerung nicht mehr
verbesserbar ist, wenn eine der folgenden Relationen eintritt:
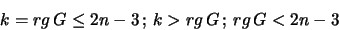 |
(1.24) |
Die physikalische Grundidee läßt sich so umsetzen:
Man stelle sich den Graphen wie oben als Stabwerk vor und
erhitze ihn. Dann dehnen sich die Stäbe aus. Treten dabei keine
inneren Kräfte auf, so ist es möglich, das System durch
Hinzufügen neuer Stäbe starr zu machen. So entsteht ein neues
Stabwerk, auf das dieselbe Prozedur immer wieder und immer wieder
angewandt wird, und zwar solange, bis keine weiteren derartigen
Veränderungen mehr möglich sind.
Bei der Betrachtung der gefundenen Graphen bemerkt man,
daß die optimalen Lagerungen - entgegen den bisherigen Fällen -
höchst unsymmetrisch sind. Zur Illustration dazu möge die
Verbesserung der Szekely'schen Konstruktion (S.27) dienen [88]:
Weitere (physikalische) Methoden [17], [47], [59], [62]
bestehen darin, die abstoßende (repulsive) Kraft, die zwischen
zwei Punkten 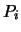 und
und 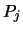 mit Abstand
mit Abstand 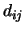 wirkt, zu minimieren.
Die abstoßende Kraft wird dabei üblicherweise mit
wirkt, zu minimieren.
Die abstoßende Kraft wird dabei üblicherweise mit
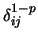 angesetzt [17]. Wandert p nach
angesetzt [17]. Wandert p nach 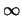 , so nähern sich die [p-]Lagerungen
der optimalen Lagerung des Unterdeckungsproblemes [60].
, so nähern sich die [p-]Lagerungen
der optimalen Lagerung des Unterdeckungsproblemes [60].
Minimiert wird üblicherweise die Gesamtenergie, das ist die
Summe über alle Interaktionen, die [47] die Darstellung hat:
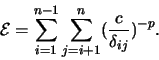 |
(1.25) |
Lokale Minima von 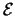 findet man durch Lösung des nichtlinearen
Gleichungssystemes
findet man durch Lösung des nichtlinearen
Gleichungssystemes
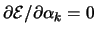 [k =1..2n].
Dabei seien die
[k =1..2n].
Dabei seien die 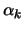 die Polarkoordinaten eines Sphärenpunktes.
die Polarkoordinaten eines Sphärenpunktes.
Damit die Lösung des Gleichungssystemes tatsächlich ein
Minimum ist, darf die Hesse'sche Matrix
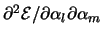 keine negativen Eigenwerte besitzen.
keine negativen Eigenwerte besitzen.
Bei der [bislang besten] Ausführung dieser Methode wählte
Kottwitz [47] eine zufällig ausgewählte Startverteilung, und
minimierte iterativ mit verschiedenen Methoden
(Gradientenmethode, Newton-Raphson), bis er ein Minimum erreichte.
So erhielt er fast optimale Lagerungen für
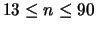 .
In der folgenden Abbildung ist das Verhalten der Dichte
.
In der folgenden Abbildung ist das Verhalten der Dichte  dargestellt:
dargestellt:
Zuletzt sollen noch einige Ergebnisse, die das
Überdeckungsproblem betreffen, erwähnt werden:
In [26] untersucht G.Fejes-Tóth dieses Problem mit einer
Methode, die der Robinson'schen [70] ähnlich ist, und löst
damit die Aufgabenstellung für 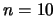 und
und 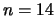 ; auch gibt er
gute Konstellationen für n = 9, 16 und 32 an.
; auch gibt er
gute Konstellationen für n = 9, 16 und 32 an.
Er stellt sich dabei die Frage, welche Polygonarten in einem
Mosaik, das durch die Mittelpunkte einer Überdeckung definiert
wird, vorkommen können und beweist, daß bei n = 10 nur vier-
und fünfkantige Ecken vorhanden sein können, bei n = 14 nur
fünf- und sechskantige.
Klarerweise kann man auch dem Überdeckungsproblem einen
Graphen zuordnen. Allerdings wird die Konstruktion etwas
aufwendiger, denn es reicht nicht, nur die Mittelpunkte zu
betrachten, man muß auch die Punkte in Betracht ziehen, die nur
durch Kreisränder bedeckt werden. Also besitzt der Graph einer
Überdeckung zwei verschiedene Ecktypen, eine gerade Anzahl von
Ecken und Kanten der Länge 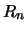 , die sich nie überschneiden.
, die sich nie überschneiden.
Auch das Tarnai'sche Temperaturprinzip funktioniert; nur muß
nun der Graph (das Stabwerk) abgekühlt werden. Dadurch zieht es
sich zusammen. Durch Entfernung der unter Druck geratenen Stäbe
und durch wiederholte Anwendung gelangt man dann zu einem
lokalen Minimum, wie Tarnai und Gáspár [90], [91], [93] bewiesen.
So wurde die bisher vollständigste Liste [93] generiert.




Nächste Seite: Diskrepanzen auf der Kugel
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Symmetrische Lagerungen, Konstruktionen
Inhalt
2004-03-25