In [6] findet sich zu diesem Problem folgender Zugang:
Es sei K ein konvexer Körper und
In [6] findet sich zu diesem Problem folgender Zugang:
Es sei K ein konvexer Körper und
![]() sei die Oberfläche der orthogonalen Projektion des Körpers
sei die Oberfläche der orthogonalen Projektion des Körpers ![]() auf die Hyperebene
auf die Hyperebene ![]() .
Ist
.
Ist ![]() der äußere Einheitsnormalvektor der Hyperebene
der äußere Einheitsnormalvektor der Hyperebene ![]() und
liegt
und
liegt ![]() in der Borelmenge der Einheitssphäre
in der Borelmenge der Einheitssphäre ![]() , so läßt sich
, so läßt sich
![]() ausdrücken durch:
ausdrücken durch:
| (3.23) |
| (3.24) |
| (3.25) |
| (3.26) |
![\begin{displaymath}
{\mathcal F}= [{\mathbf x}_{\sigma (1)} ] +..+ [{\mathbf x}...
...gma (r+1)} /2 +..+ (\pm 1) \cdot {\mathbf x}_{\sigma (n)} /2,
\end{displaymath}](img962.gif)
| (3.27) |
| (3.28) |
| (3.29) |
| (3.30) |
| (3.31) |
| (3.32) |
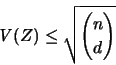 |
(3.33) |
| (3.34) |
| (3.35) |