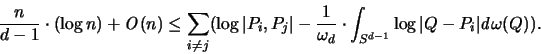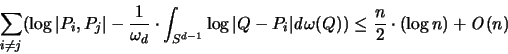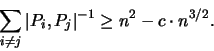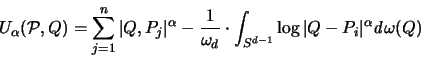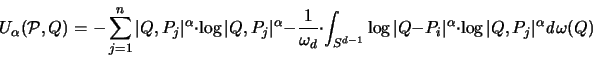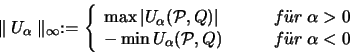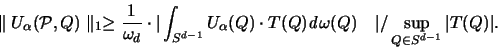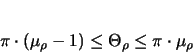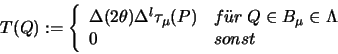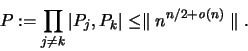Nächste Seite: Approximation der Kugel durch
Aufwärts: Diskrepanzen auf der Kugel
Vorherige Seite: Invarianzprinzip
Inhalt
Nachdem wir die Potenzsumme für 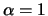 abschätzen konnten,
wollen wir eine Abschätzung der Summe in beide Richtungen
für
abschätzen konnten,
wollen wir eine Abschätzung der Summe in beide Richtungen
für
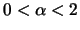 angeben.
angeben.
Wie im vorigen Paragraphen wird auch hier die Potenzsumme
mit dem zu erwartenden Mittelwert in Verbindung gesetzt, den
wir so definieren:
Es sei
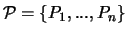 eine Menge von n Punkten auf
eine Menge von n Punkten auf 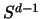 ,
,
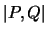 sei der Euklidische Abstand.
sei der Euklidische Abstand.
Für 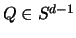 ,
,
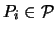 und die Kernfunktion
und die Kernfunktion
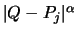 ist der gesuchte Mittelwert für
ist der gesuchte Mittelwert für 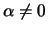 :
:
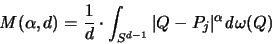 |
(2.21) |
Es gilt der folgende Satz [96, 99]:
Für 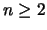 und für
und für
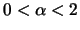 gibt es eine n-elementige
Punktmenge
gibt es eine n-elementige
Punktmenge
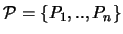 und gibt es vier positive Konstante
c, c', k und k', die alle nur von
und gibt es vier positive Konstante
c, c', k und k', die alle nur von 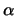 und d abhängen, sodaß gilt:
und d abhängen, sodaß gilt:
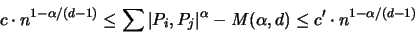 |
(2.22) |
Weiters gilt für
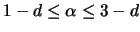 :
:
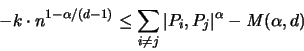 |
(2.23) |
und für
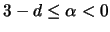 und
und 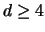 gilt:
gilt:
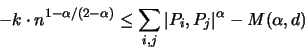 |
(2.24) |
[Man kann zeigen, daß die Ungleichung (3) bestmöglich ist.]
Für 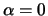 gilt:
gilt:
Umgekehrt gilt die Ungleichung:
Der Satz beinhaltet für 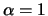 das Ergebnis von (II.5), sowie für
die Verteilung von n Elektronen auf
das Ergebnis von (II.5), sowie für
die Verteilung von n Elektronen auf  :
:
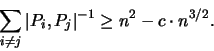 |
(2.25) |
Eng verwandt mit den Potenzsummen, die man auch als
Energiesummen betrachten kann [96], sind Potentiale [96],[99], die
für
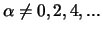 definiert sind durch:
definiert sind durch:
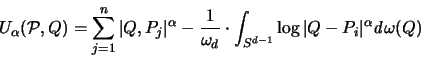 |
(2.26) |
und für
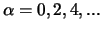 durch:
durch:
Für diese gilt [Satz 2 in [97], Theorem A in [99]]:
Es gibt für 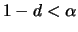 , aber
, aber
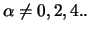 Konstante C und c,
die nur von
Konstante C und c,
die nur von 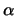 und
und 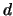 abhängen, sodaß gilt:
abhängen, sodaß gilt:
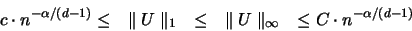 |
(2.27) |
Unter
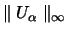 wollen wir dabei
folgendes verstehen:
wollen wir dabei
folgendes verstehen:
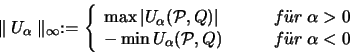 |
(2.28) |
wobei wir über alle 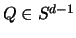 maximieren bzw. minimieren.
maximieren bzw. minimieren.
Da die beiden Funktionale zusammenhängen, beschränken wir
uns hier auf eine Beweisskizze der Aussage (2.27).
Der Beweis der linken Seite von (2.27) benützt wieder die harmonische Analyse
auf der Sphäre. Die Grundidee besteht darin, eine Testfunktion T zu
konstruieren, die folgende Ungleichung erfüllt :
Wir führen auf 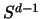 Polarkoordinaten ein und betrachten
die Differentialgleichung
Polarkoordinaten ein und betrachten
die Differentialgleichung
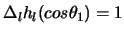 .
Dabei ist
.
Dabei ist  der Laplace-Operator und
der Laplace-Operator und 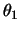 die erste
Polarkoordinate des Punktes
die erste
Polarkoordinate des Punktes  :
:
Für eine gegebene Punktmenge
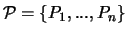 definieren wir
definieren wir
 durch
durch
 und betrachten die Funktion:
und betrachten die Funktion:
Nun zerlegen wir 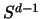 in Rechtecke
in Rechtecke 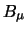 der Form:
der Form:
Dabei gibt
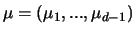 die Begrenzung des Rechteckes
die Begrenzung des Rechteckes 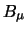 an. Es ist daher mit
an. Es ist daher mit
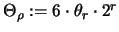 :
:
Es sei nun
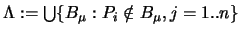 die Menge aller Rechtecke, die keinen Punkt der Menge
die Menge aller Rechtecke, die keinen Punkt der Menge 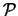 enthalten.
Durch die Wahl von r kann man erzwingen, daß
enthalten.
Durch die Wahl von r kann man erzwingen, daß
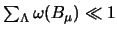 ausfällt, da man
die Rechtecke beliebig klein machen kann.
ausfällt, da man
die Rechtecke beliebig klein machen kann.
Für jeden Punkt
 sei
sei
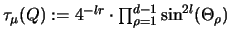 .
.
Dann können wir die gewünschte Testfunktion definieren:
Es gilt:
Es sei
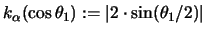 ;
;
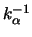 sei die zu
sei die zu 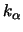 in Bezug
auf das Faltungsprodukt inverse Funktion, das ist die
Funktion, für die gilt:
in Bezug
auf das Faltungsprodukt inverse Funktion, das ist die
Funktion, für die gilt:
Im letzten Beweisschritt für (7) verwendet man
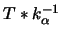 als
Testfunktion für
als
Testfunktion für
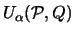 und wertet hier übergangene
Ungleichungen aus [96].
und wertet hier übergangene
Ungleichungen aus [96].
Auch für den Beweis der rechten Seite wird 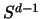 in Rechtecke
in Rechtecke
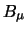 zerlegt. Auf diese Rechtecke wird die Beck'sche Methode aus
II.2 angewandt. Daher muß für sie gelten:
zerlegt. Auf diese Rechtecke wird die Beck'sche Methode aus
II.2 angewandt. Daher muß für sie gelten:
Für
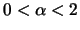 halten wir einen Punkt
halten wir einen Punkt 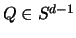 fest und wenden
auf die Rechtecke
fest und wenden
auf die Rechtecke 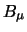 den zentralen Satz von II.5 an. Dadurch
erhalten wir Interpolationspunkte
den zentralen Satz von II.5 an. Dadurch
erhalten wir Interpolationspunkte
 .
Es sei B die konvexe Hülle der Bereiche, in denen
Interpolationspunkte liegen. Weiters teilen wir die Rechtecke
.
Es sei B die konvexe Hülle der Bereiche, in denen
Interpolationspunkte liegen. Weiters teilen wir die Rechtecke 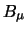 durch
folgende Bedingung in Klassen
durch
folgende Bedingung in Klassen 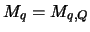 (q = 0,1,..) ein:
(q = 0,1,..) ein:
Wegen
 kann jede Klasse
kann jede Klasse 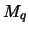 maximal
maximal
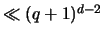 Rechtecke enthalten.
Rechtecke enthalten.
Für jeden Bereich
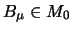 ist
ist
Für die Bereiche 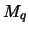 mit
mit 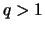 kann man mittels Taylorreihe
zeigen, daß:
kann man mittels Taylorreihe
zeigen, daß:
Addiert man diese beiden Ergebnisse zusammen, und beachtet
man, daß
 ist, so erhält man:
ist, so erhält man:
Anstelle von Abstandssummen [weitere Beispiele findet man in
[102]-[104]] kann man Produkte von Abständen betrachten [97]:
Ist
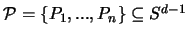 so gilt [97] für
so gilt [97] für
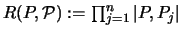 :
:
(P ist im folgenden stets ein Punkt auf 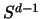 )
)
Für eine unendliche Folge
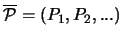 sei
sei
Dann ist für 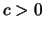 und unendlich viele Werte von n:
und unendlich viele Werte von n:
Es ist weiters:




Nächste Seite: Approximation der Kugel durch
Aufwärts: Diskrepanzen auf der Kugel
Vorherige Seite: Invarianzprinzip
Inhalt
2004-03-25
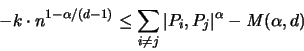
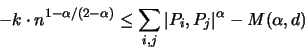
![]() gilt:
gilt: